Сред нашия народ отдавна са добили популярност един особен вид задачи, които са били разказвани по разни поводи. Това са задачи с различна степен на трудност, но облечени в ярка занимателна и лесно възприемаща се форма. Те се били разказвани наред с приказките, пословиците и гатанките. Основната цел на тези задачи е била не толкова забавлението, колкото проверката на способността на хората за остроумни разсъждения, съобразителност и досетливост. Задаването и решаването на такива задачи е доставяло не по-малко удоволствие от това, получавано при изпълнение на народни песни и танци, при разказване на приказки и други. Както при другите видове народно творчество за този вид задачи са характерни анонимност на авторите и устна форма на разпространение. Всичко това дава основание да говорим за задачи от народното творчество или за задачи от математическия фолклор.
В продължение на предишните 2 статии и в тази с удоволствие ви представяме още 7 задачи от народния фолклор. Техните отговори и решения можете да намерите най-отдолу в статията.
Задачи
- В една кутия има 1 кг и 100 г чай. Трябва да отсипем точно 1 кг като разполагаме с 2 други кутии, едната от които побира точно 300 г, а другата – 650 г. Как да постъпим?
- Имаме 3 съда съответно от 8 л, 5 л и 3 л. Най-големият съд е пълен с мляко. Как може да разделите млякото от него по равно на две, като използвате само тези три съда?
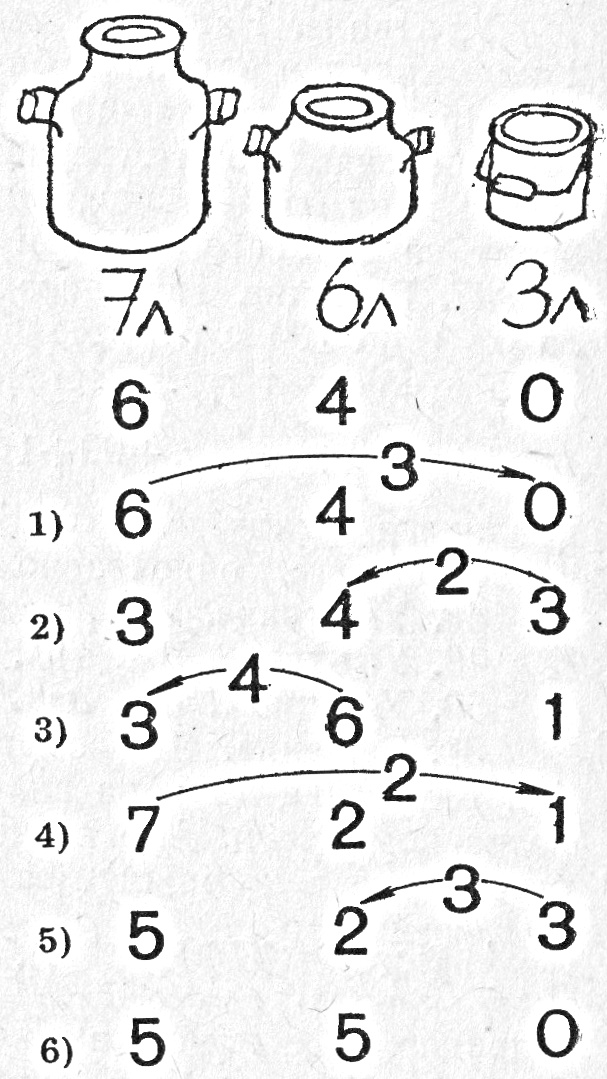
- Двама селяни имали по равен брой овце. Издоили ги в едно ведро от 10 оки и го напълнили. Те нямали други съдове, освен още едно ведро, което събирало 3 оки, и друго – от 7 оки. Как са постъпили селяните, за да си разделят по равно млякото?
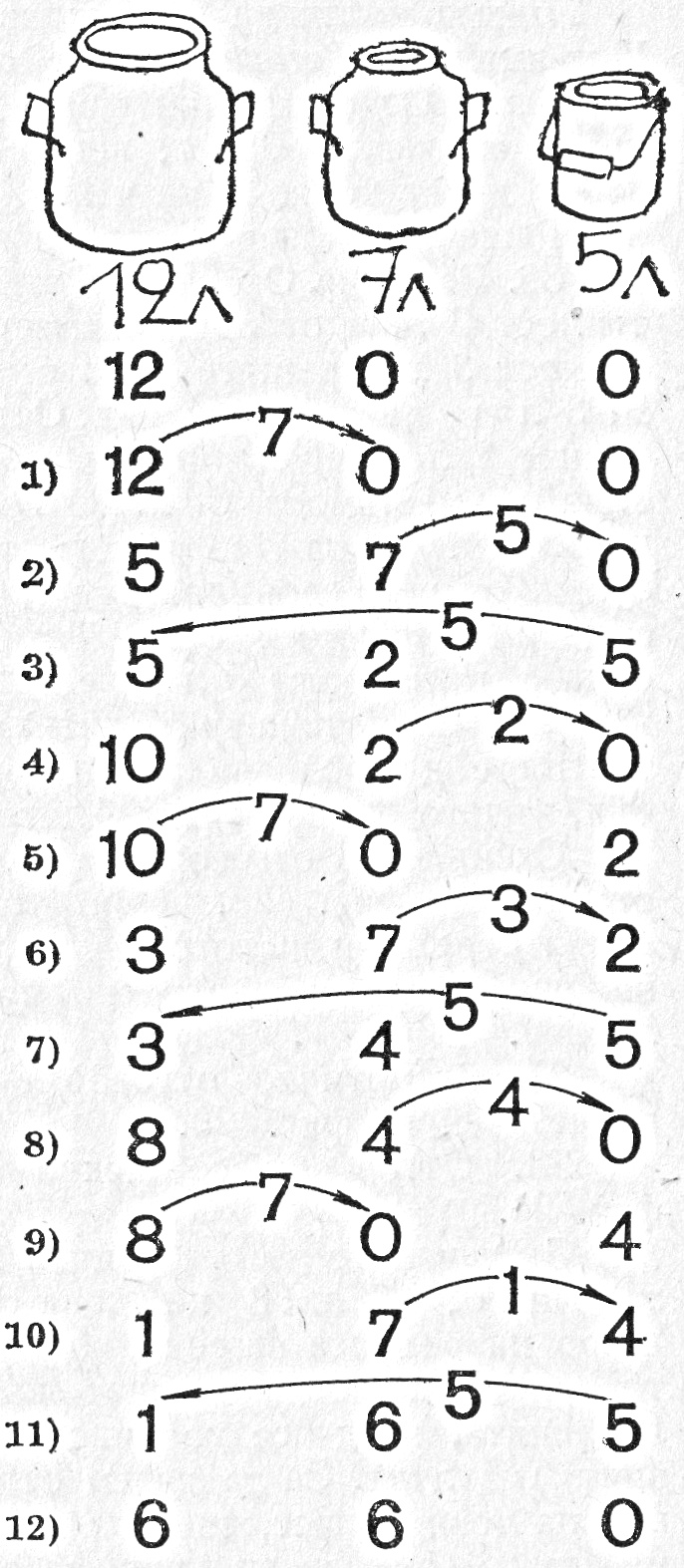
- Овчар имал само 3 съда – единият събирал 12 л, другият – 7 л, а третият – 5 л. Най-големият съд бил пълен с мляко, а другите два – празни. Как може овчарят да раздели млякото на 2 равни части?

- Нека са дадени 3 съда с обеми съответно p, q и r така, че p+q=r. Съдът с обем r е пълен с течност, а другите два са празни. Като се използват само трите съда, да се раздели течността на 2 равни части (p, q и r са цели числа).
- Двама овчари трябвало да си разделят по равно 14 л мляко, което било в съд от 16 л. Те разполагали с още 2 съда – единият от 8 л, а другият – от 5 л. Как могат да си разделят млякото двамата овчари, като използват само тези 3 съда?
- Има 3 съда с вместимост съответно 6 л, 3 л и 7 л. В първия съд има 4 л, а в третия – 6 л мляко. Да се раздели млякото на 2 равни части, като се използват само тези 3 съда.
За още интересни статии и задачи от света на математиката, разгледайте нашия блог. Ако искате да положите и надградите знанията си по математика и да развиете логическото си мислене, за да можете да решавате и други подобни задачи от необятния свят на математиката, разгледайте нашия курс "Математика за програмисти - част 1". Той е фокусиран върху най-важните теми в математиката и приложението им в програмирането. В ресурсите има над 13 часа видео лекции и над 220 страници PDF книжка.
Отговори и решения
- Решение: Да означим с I, II и III пакетите с вместимост 1100 г, 650 г и 300 г. Последователните пресипвания ще изобразим с помощта на следната таблица:
И така, след 12 пресилвания в I пакет има 1 кг чай.I 1100 450 450 750 750 1050 1050 400 400 700 700 1000 II 0 650 350 350 50 50 0 650 400 400 100 100 III 0 0 300 0 300 0 50 50 300 0 300 0
Бихме могли да разсъждаваме и така. От I пълним II, а от II пълним III. Тогава във II остават 350 г, които изсипваме настрани. От останалия чай в I и III пълним II пакет, т. е. отново получаваме 650 г, които заедно с отмерените преди това 350 г дават точно 1 кг чай.
Решението е представено и на фигурата по-долу: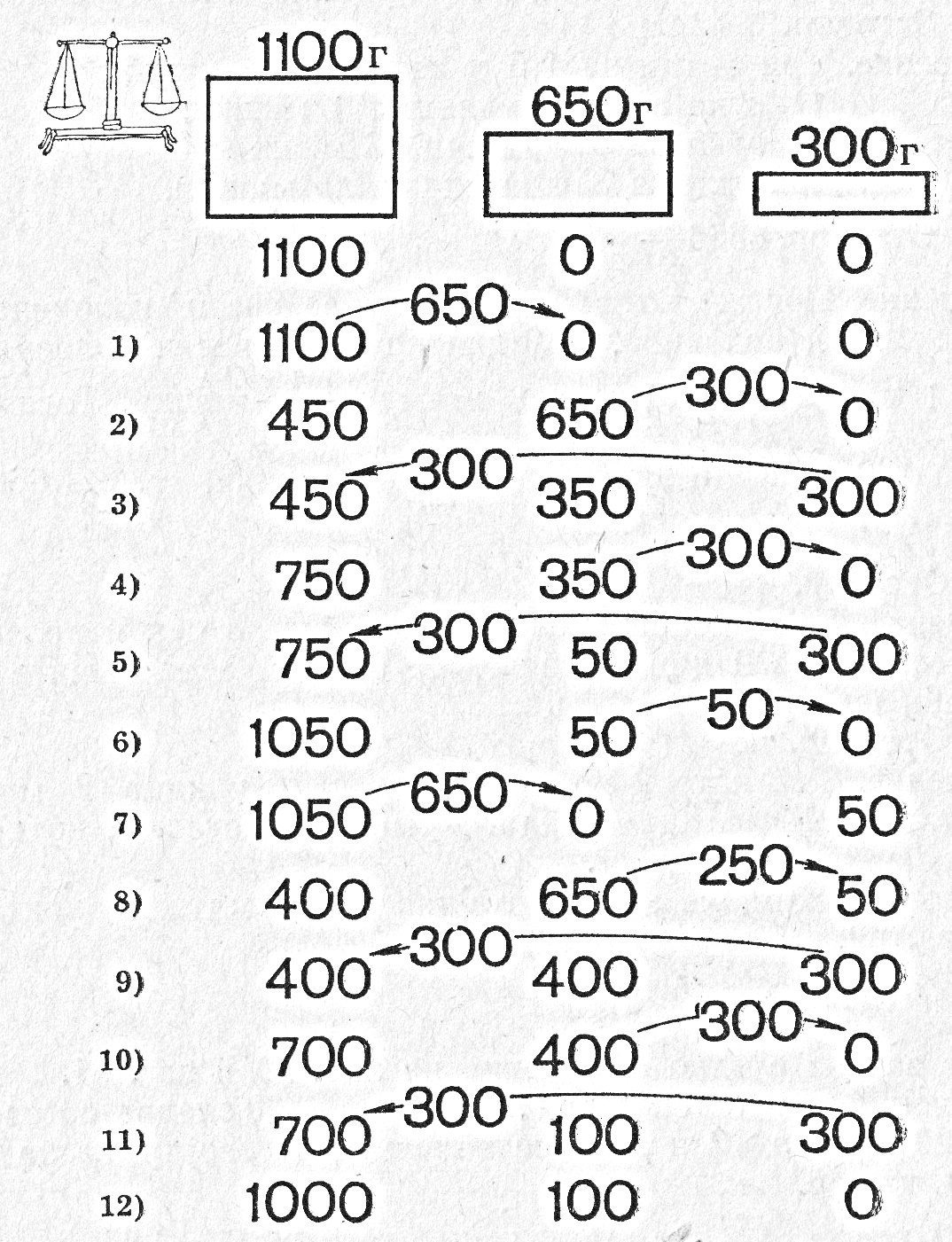
- Решение: От съда с вместимост 8 л напълвате съда с вместимост 5 л, а от съда с вместимост 5 л напълвате съда с вместимост 3 л. Връщате отново тези 3 л в най-големия съд. Останалите 2 л от II съд преливате в съда с вместимост 3 л. Отново напълвате съда с вместимост 5 л и от него допълвате с 1 л съда с вместимост 3 л. Така в съда с вместимост 5 л вече остават 4 л. След това трите литра от третия съд преливаме в първия съд, където също стават 4 литра. Схематично отговорът е представен на фигурата по-долу:
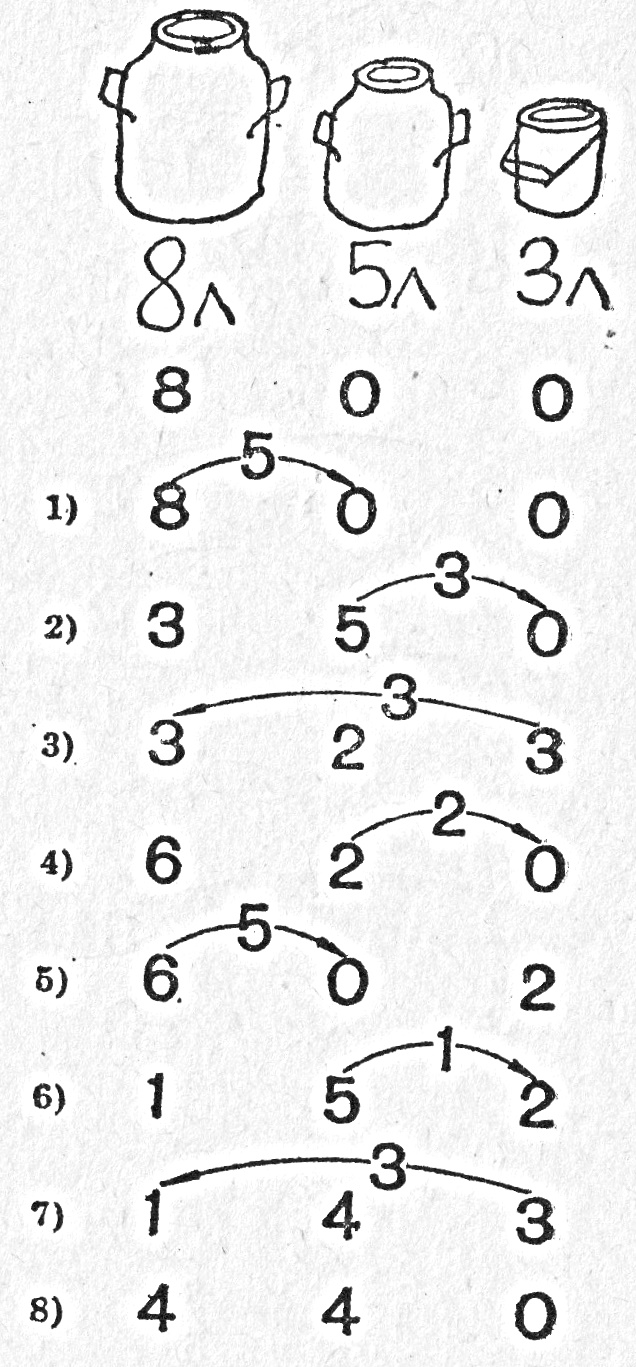
- Решение: Схематично решението е представено на фигурата по-долу:
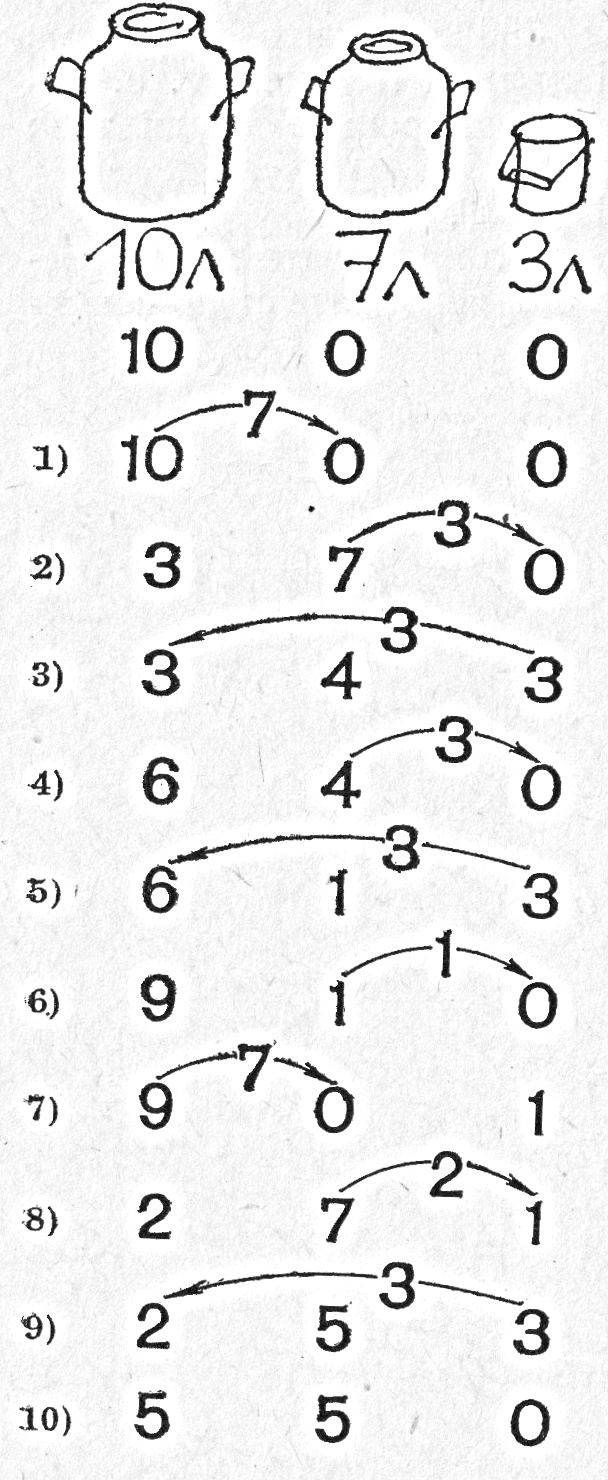
- Решение: Схематично решението е представено на фигурата по-долу:
Съставянето на таблиците за задачи 2, 3 и 4 не дава отговор на въпроса за реда, по който трябва да се извършат преливанията, за да се получи желаният резултат. За да дадем отговор на този въпрос, ще разгледаме един геометричен начин за решаване на зад. 2. Да означим с x и y количеството течност, съдържащо се след всяко преливане съответно в първия и втория съд. Тогава тя в третия съд винаги е 8–x–y. Числата x, y, 8–x–y са цели и удовлетворяват неравенствата:
При дадена правоъгълна координатна система x O y на всяка двойка стойности на x и y отговаря точка от равнината (фигурата по-долу)0 ≤ x ≤ 8 0 ≤ x ≤ 8 0 ≤ y ≤ 5 ⇔ 0 ≤ y ≤ 5 0 ≤ 8–x–y ≤ 3 5 ≤ x + y ≤ 8
Всички точки, чиито координати удовлетворяват записаните условия, са точки от успоредника ABCD. На началното разпределение на течността отговаря точката B (8; 0), а на желаното разпределение отговаря точката M (4; 4).
Може да се установи, че последователността от преливания, водеща от разпределението B до разпределението M, се представя с точки от успоредника ABCD. Ако съединим с отсечки всеки две последователни точки, ще се получи начупена линия с начало B и край M.
Да разгледаме по-подробно условията, на които отговарят върховете и отсечките на разглежданата начупена линия. Тези условия ще ни подскажат как можем с геометрични средства да решаваме задачи, аналогични на разглежданата. Да проследим начупената линия. Ще установим, че на разпределението, при което вторият съд е празен, отговарят точките от отсечката AB с абсциси съответно 5, 6, 7 и 8, а на разпределението, при което вторият съд е пълен, отговарят точките от отсечката DC с абсциси съответно 0, 1, 2 и 3. На разпределението, при което третият съд е празен, отговарят точките от отсечката BC съответно с координати (8;0), (7;1), (6;2), (5;3), (4;4) и (3;5). Най-накрая на разпределението, при което третият съд е пълен, отговарят точките от отсечката AD съответно с координати (5;0), (4;1), (3;2), (2;3), (1;4) и (0;5). Следователно върховете на начупената линия са точки от контура на успоредника ABCD.
Тъй като при всяко преливане течността в един от съдовете не се променя, възможни са следните случаи:
а) ако не се променя течността в първия съд, то отсечката, съединяваща точките, съответстващи на разпределението преди и след преливането, е успоредна на оста Oy;
б) ако не се променя течността във втория съд, то отсечката, съединяваща точките, съответстващи на разпределението преди и след преливането, е успоредна на оста Ox;
в) ако в преливането не участва третият съд, то се запазва общото количество течност x+y в първите два съда, което означава, че отсечката, съединяваща точките преди и след преливането, е успоредна на BC; по-точно, ако третият съд е пълен, отсечката е подмножество на отсечката AD, а ако е празен, тя е подмножество на BC и обратно.
И така, всяка отсечка от начупената линия или е успоредна на оста Ox, или е успоредна на оста Oy, или е успоредна на отсечката BC (включително и нейно подмножество, когато третият съд е празен). Освен това, ако третият съд е пълен, т. е. x+y=5, то преливането на първия съд във втория завършва, когато x=0 и y=5, а преливането от втория в първия – когато x=5 и y=0. Това означава, че на тези случаи съответстват точките D и A. Аналогично се установява, че ако някоя от другите отсечки е подмножество на страна на успоредника ABCD, то непременно неин край съвпада с някоя от точките A, B, C или D.
Тъй като на началния момент от процеса на преливането отговаря точката B (8;0), а на крайния — точката M (4;4), на геометричен език целта на задачата може да се изкаже така: „Да се съедини точката B с точката M чрез начупена линия, върховете на която лежат на контура на успоредника, а всяка от отсечките й е успоредна на някоя от координатните оси или на отсечката BC. При това, ако някоя отсечка от начупената линия е част от страна на успоредника, то неин край трябва да съвпада с връх на успоредника.“
Създаденият по този начин геометричен модел позволява задачата да се реши без много затруднения, като се използва координатна система. Чрез няколко опитвания се начертава начупената линия така, че върховете и страните й да отговарят на посочените условия.
Така на следващата фигура е намерено второ решение на задача 2.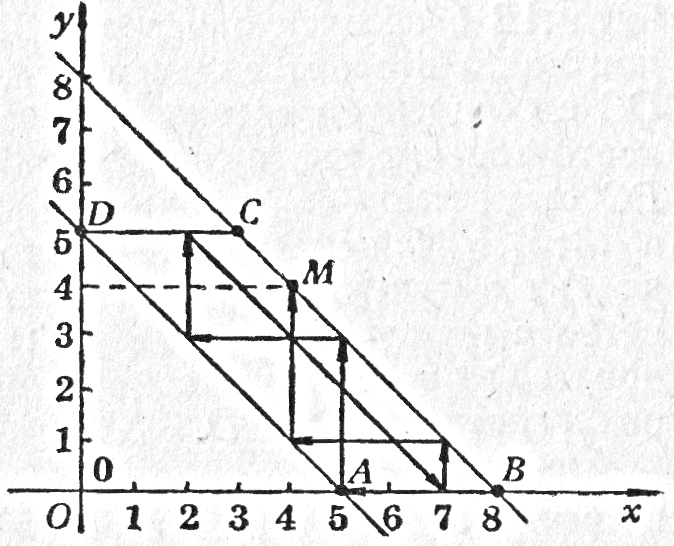
Броя на опитите можем да намалим, като предварително изчислим минималния брой отливания от първия съд в един от другите съдове и минималния брой отливания от останалия (трети) съд, и то по толкова течност, колкото побира всеки от тях (ще казваме цяло преливане).
За целта да означим например с m броя на „целите“ отливания от първия съд във втория и с n – броя на целите отливания от третия съд във втория. Тогава според изискването в задачата: 8 – 5m + 3n = 4. Като използваме, че m = (4 + 3n) / 5 лесно намираме първата двойка цели решения на полученото уравнение, а именно (2; 2). - Решение: Тази задача е обобщение на задачи 2, 3 и 4.
Да означим с m броя на целите отливания от съда с обем r в съда с обем p и с n – броя на целите отливания от съда с обем q в съда с обем r. Тогава според изискването в задачата:
r – mp + nq = r/2 ⇔ 2mp – 2nq = r
От последното равенство, като заместим r с p+q, получаваме:0
2mp – 2nq = p + q
p = ((2n + 1) q) / (2m – 1)
Тъй като m, n, p и q са цели числа, като използваме последната формула, можем да получаваме различни подходящи наредени четворки, въз основа на които не само да съставяме конкретни задачи, но и предварително да знаем броя на целите преливания, чрез които може да се реши задачата. Понеже случаят, когато m=1, е тривиален, ще дадем някои четворки при m > 1:
Не е трудно да се види за кои от получените случаи се отнасят съответно зад. 2, зад. 3 и зад. 4.m=2, q=3, p=2n+1
m=2, q=3, n=1, p=3 (r=6)
m=2, q=3, n=2, p=5 (r=8)
m=2, q=3, n=3, p=7 (r=10)
m=2, q=3, n=4, p=9 (r=12)
………………………m=2, q=6, p=2(2n+1)
m=2, q=6, n=1, p=6 (r=12)
m=2, q=6, n=2, p=10 (r=16)
………………………m=3, q=5, p=2n+1
m=3, q=5, n=1, p=3 (r=8)
m=3, q=5, n=2, p=5 (r=10)
m=3, q=5, n=3, p=7 (r=12)
……………………… - Решение: Схематично решението е представено на фигурата по-долу:
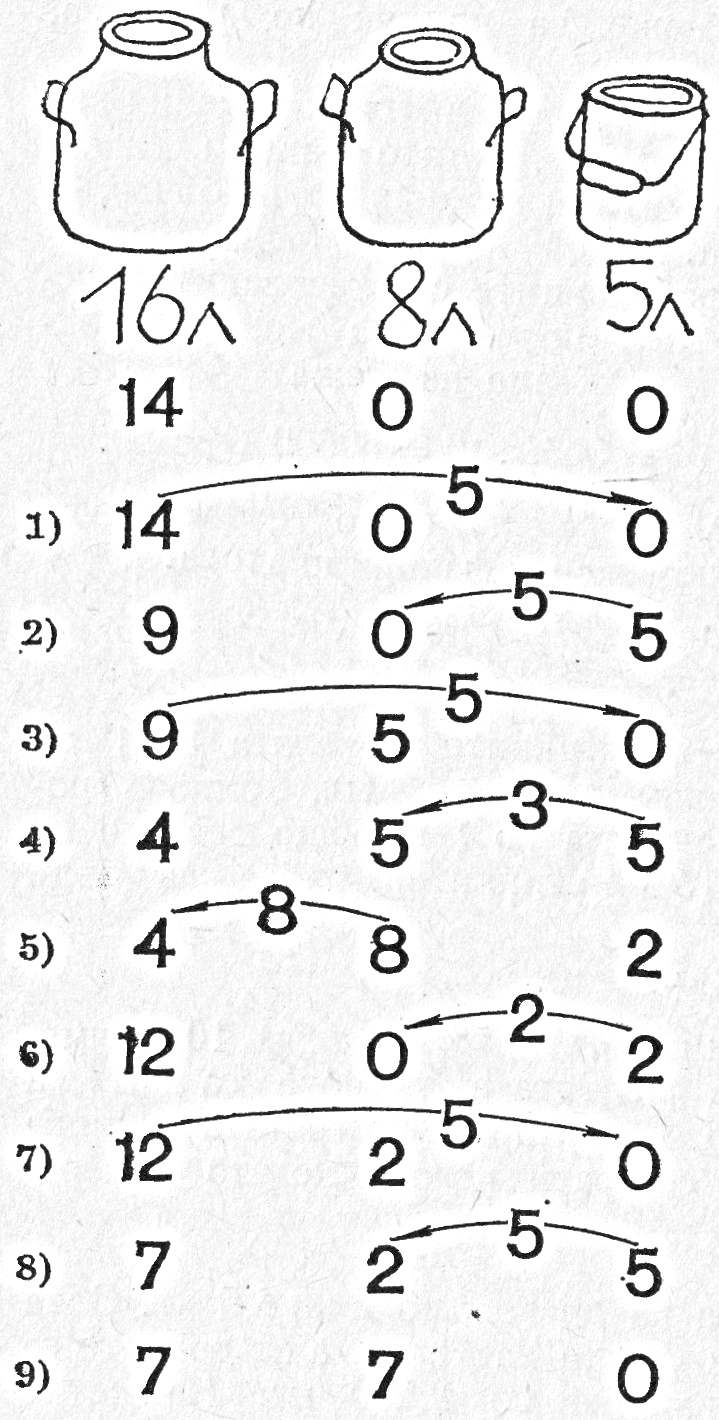
- Решение: Схематично решението е представено на фигурата по-долу: