Програмирането е немислимо да съществува без основните принципи и теории на приложната математика. Така например, широк кръг от задачите на програмирането са свързани с простите числа. А простите числа, от своя страна, много често са обвързани с теорията за Решето на Ератостен. Решето на Ератостен е познато на математиците от векове насам. В програмирането то намира още по-значимо приложение. Редица алгоритми са свързани с него, защото самото Реше на Ератостен е вид алгоритъм. Ето защо в този материал решихме да ви запознаем с него, като ви го разясним максимално простичко и ясно.

Но първо – кой е Ератостен?

Ератостен често е определян като един от най-великите европейци. Според историческите извори, той е роден през 276 година преди Новата Ера в района на Киренайка, чиято територия днес е заемана от развитие части на Либия. Ератостен проявява интерес към математиката от най-ранно детство, когато усилено учи естествени и точни науки в Атина. След като виждат огромния му потенциал, той бива поканен в Александария, за да поеме възпитателните функции на Птолемей Четвърти, следващият елински престолонаследник. Така Ератостен само след няколко години се превръща в основно лице на научната школа в Александрийската библиотека, която е била и средището на математиката, географията и астрономията в Древността.

Числата привличат Ератостен изключително силно и преди да създаде своя алгоритъм за решето на простите числа, той се опитва да измери големината на Земята. Всъщност, Ератостен е и първият човек на планетата, който се опитва да разреши тази задача.

Ератостен е първенец и в друго направление. Това е първият човек, който пише сборник „География“ с фундаментални принципи и открития в това направление.

Но и до ден днешен, Ератостен винаги е бил свързван главно и основно с неговите огромно значение за съвременната математика. И естествено, Решето на Ератостен е голямото откритие на учения. В редовете по-долу ще видите какво точно представлява този алгоритъм.

Какво представлява Решето на Ератостен?

Решето на Ератостен се свързва с огромна част от дискусиите относно теорията на числата. Самото Реше представлява теория, но едновременно с това и алгоритъм, използван за откриване на зависимости и редове от прости числа. На практика, Ератостен създава този алгоритъм именно в търсене на простите числа.

Какво обаче е простото число? Без да се припомним това определение, няма смисъл да продължаваме да разясняваме и самия алгоритъм за решаване на задачи с прости число. Просто число представлява едно положително цяло число. То е по-голямо от едно и не се дели на никое друго число, освен на 1 и на себе си.

Какво се е опитал да направи Ератостен? Неговата цел била да открие всички прости числа в интервал от 1 до n, където n да е което и да е естествено число. Предложеният от него алгоритъм е толкова ефикасен, че стотици години по-късно той продължава да бъде използван. Разбира се, новите модели са видоизменени по-посока опростяване и най-вече спестяване на време за решаване на задачата. На практика обаче всеки следващ алгоритъм следва този на Ератостен, тоест Решето на Ератостен.

А как точно ги открива Ератостен? Как работи методът на Решето?

Ератостен  използва думата „решето“, защото във формата на решетка изписва възможните числа, които биват обаче задрасквани, ако не отговарят на условието да бъдат прости числа. Всички незадраскани числа на практика остават като прости. След като премахва 1, Ератостен  започва от 2 и задрасква всяко второ число, вървейки отляво надясно, без да бъде задрасквана двойката. Следващата му стъпка е да намери първото нездраскано число поред след двойката.  Това, разбира се, е тройката, поради което следващото задраскано число ще бъде всяко трето след, отново вдясно. Редът се получава като остане низ от много незадраскани числа k и като се задраска всяко следващо k поред число, вървейки от ляво на дясно. 

Казано по друг начин, Ератостен задрасква всички числа, които се делят на 2, а след това тези – на 3 и продължава по същата логика, докато зачеркне всички възможни числа. На практика обаче той не може да зачеркне числата, делящи се на 4, защото те се делят на 2. В крайна сметка, Ератостен  задрасква само числата, които се делят на прости числа и не са по-големи от квадратен корен от числото, възприето за горна граница на търсенето.

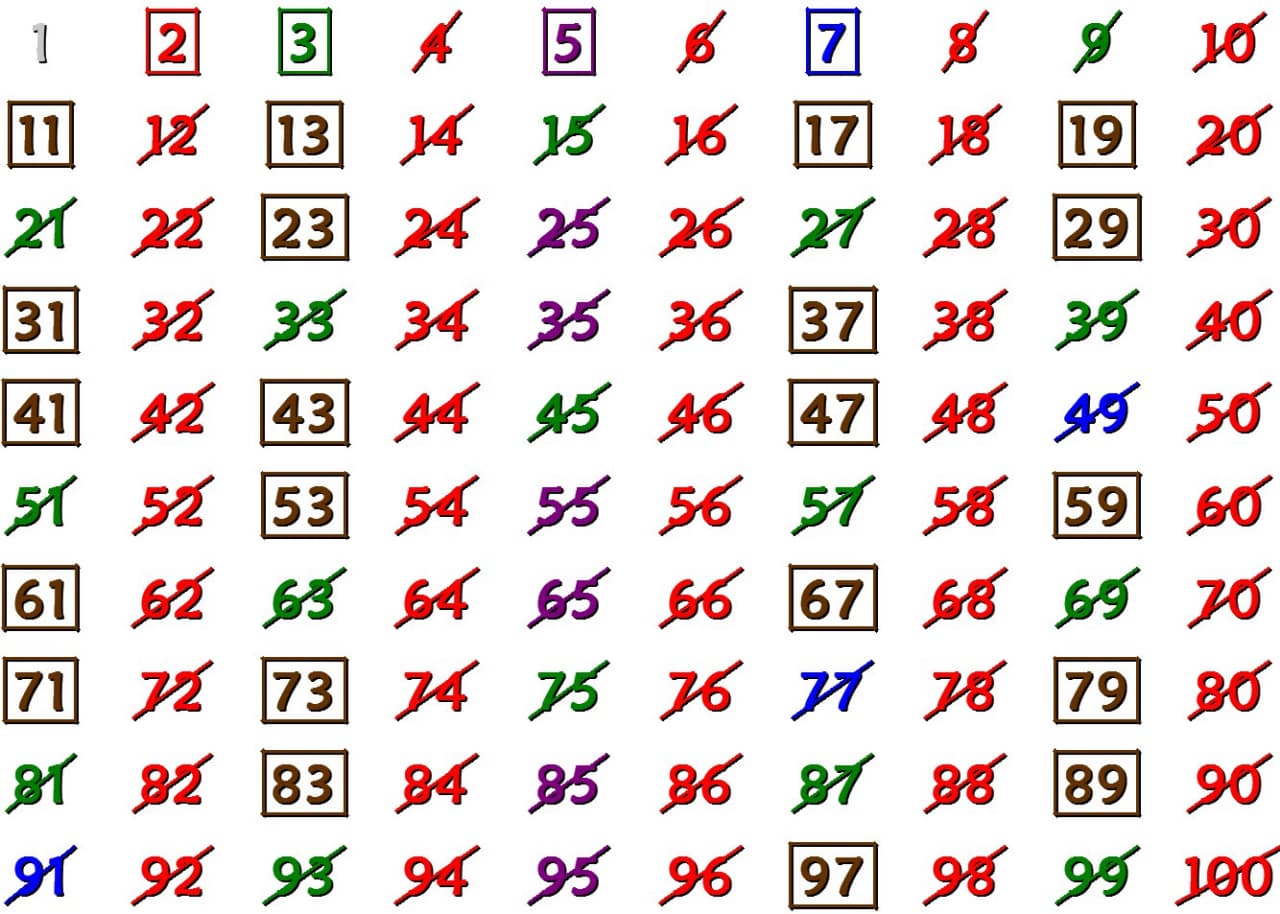
Изводи от метода на Решето на Ератостен

Това не са толкова изводи, колкото изведени свойства за простите числа според алгоритъма на Ератостен. Веднага след появата на алгоритъма, а и векове по-късно математиците използва Решето на Ератостен, за да обобщят следните свойства:

• Не съществува такова нещо като най-голямо просто число. Изводът се прави чрез невъзможност за доказване на обратното предположение. Най-голямото пресметнато до този момент просто число е 232,582,657 − 1.
• На практика, не могат да се преброят всички прости числа. Броят им е безкраен. До този извод се стига след размишления относно предишното свойство.
• Всяко естествено число, което е по-голямо от 1, би могло да е представено по свой собствен начин под формата на произведение от ред от няколко ненамаляващи прости числа. Това свойство, изведено от Решето на Ератостен днес познаваме на Теорема на аритметиката.

Решето на Ератостен намира изключително широко приложение в програмирането и криптирането, тъй като те ползват и силно зависят от функциите на естествените числа. Съвременната математическа наука продължава да се ползва от този алгоритъм, като нейните най-значими и активни имена смятат, че Решето на Ератостен има не просто историческа стойност, но и реално бъдеще.

Курс по математика за програмисти

Ако имате нужда от още и още от знанията в сферата на математиката, които са силно свързани с програмирането, напомняме ви, че при нас можете да ги получите по най-удачния начин. Ще видите на практика и показана от истински практици голямата връзка и зависимост между математиката и програмирането.

Курсът "Математика за програмисти - част 1" е фокусиран над най-важните теми в математиката и програмирането.  Към ресурсите влизат над 13 часа видео лекции и над 220 страници PDF наръчник.

Лектор е Николай Костов (Solutions Architect в ZenCodeo) – специалист с опит като софтуерен инженер (над 15 години), обучител (над 10 години) и дългогодишен участник и победител в редица състезания по информатика и информационни технологии. Ники има голям брой успешно положени изпити и сертификати (включително трейнърският сертификат Microsoft Certified Trainer без прекъсване от 2014 г. до 2021 г., включително). Студент на годината (2015 г.) и награден от Forbes Bulgaria с наградата “30 под 30” в категория образование (2015 г.). Съавтор в няколко книги и има стотици проведени лекции и записани видеа по програмиране.

Линк към курса: "Математика за програмисти - част 1"